This is the last of a 10-part series on building high-quality assessments.
- Part 1: Quality Factors
- Part 2: Standards and Content Specifications
- Part 3: Items and Item Specifications
- Part 4: Item Response Theory, Field Testing, and Metadata
- Part 5: Blueprints and Computerized-Adaptive Testing
- Part 6: Achievement Levels and Standard Setting
- Part 7: Securing the Test
- Part 8: Test Reports
- Part 9: Frontiers
- Part 10: Scoring Tests

Lillian takes an exam and gets a score of 83%. Roberta takes an exam and achieves 95%. Are these comparable scores? A fraction of what was achieved in each case?
Suppose Lillian's exam was the final in College Thermodynamics. A score of 83% means that she earned 83% of the maximum possible score on the test. In traditional scoring, teachers assign a certain number of points to each question. A correct answer earns the student all points on that question. Incorrect earns zero points. And a partly correct answer may earn partial points.
Roberta's exam was in middle school Algebra. Like Lillian, her score is represented as a fraction of what can be achieved on that particular exam. Since these are different exams in different subject areas and different difficulty levels, comparing the scores isn't very meaningful. All you can say is that each student did well in her respective subject.
Standardized Scoring for Quality Assessment
This post is a long overdue coda to my series on quality assessment. In part 4 of the series, I introduced item response theory (IRT) and how items can be calibrated on a continuous difficulty scale. In part 6 I described how standardized test scores are mapped to a continuous scale and interpreted accordingly.
This post is a bridge between the two. How do you compute a test score from a calibrated set of IRT questions and put it on that continuous scale?
Calibrated Questions
As described in part 4, a calibrated question has three parameters. Parameter a represents discrimination, parameter b represents difficulty, and parameter c represents the probability of getting the question right by guessing.
Consider a hypothetical test composed of five questions, lettered V, W, X, Y, and Z. Here are the IRT parameters:
| Item | V | W | X | Y | Z |
|---|---|---|---|---|---|
| a | 1.7 | 0.9 | 1.8 | 2.0 | 1.2 |
| b | -1.9 | -0.6 | 0.0 | 0.9 | 1.8 |
| c | 0.0 | 0.2 | 0.1 | 0.2 | 0.0 |
Here are the five IRT graphs plotted together:

The horizontal dimension is the skill level on what psychometricians call the "Theta" scale. The usable portion is from approximately -3 to +3. The vertical dimension represents the probability that a student of that skill level will answer the question correctly.
All of the graphs in this post, and the calculations that produce them are in an Excel spreadsheet. You can download it from here and experiment with your own scenarios.
Adding Item Scores
When the test is administered, the items would probably be delivered in an arbitrary order. In this narrative, however, I have sorted them from least to most difficult.
For our first illustration the student answers V, W, and X correctly, and they answer Y and Z incorrectly. For answers they get correct, we plot the curve directly. For answers they get incorrect, we plot (1 - y) which inverts the curve. Here's the result for this example.

Now, we multiply the values of the curves together to produce the test score curve.
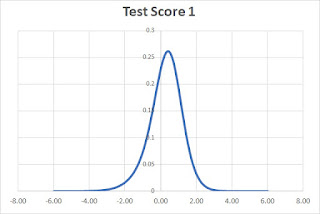
The peak of the curve is at 0.4 (as calculated by the spreadsheet). This is the student's Theta Score for the whole test.
Scale Scores
As mentioned before, the Theta Score is on an arbitrary scale of roughly -3 to +3. But that scale can be confusing or even troubling to those not versed in psychometrics. A negative score could represent excellent performance but, to a lay person, it doesn't look good.
To make scores more relatable, we convert the Theta Score to a Scale Score. Scale scores are also on an arbitrary scale. For example, the ACT test is mapped to a scale from 1 to 36. SAT is on a scale from 400 to 1600 and the Smarter Balanced tests are on a scale from 2000 to 3000.
For this hypothetical test we decide the scale score should range from 1200 to 1800. We do this by multiplying the Theta Score by 100 and adding 1500. We describe this as having a scaling function with slope of 100 and intercept of 1500.
In this illustration, the Theta Score of 0.4 results in a scale score if 1540.
Another Example
We have another student that's less consistent with their answers. They get questions X and Z correct and all others incorrect.

In this case, the peak is at -0.6 which results in a scale score of 1440.
Confidence Interval - Standard Error
In addition to a Scale Score, most tests report a confidence interval. No test is a perfect measure of a student's true skill level. The confidence interval is the range of scores in which the student's true skill level should lie. For this hypothetical test we will use a 90% interval which means there is a 90% probability that the student's true skill level lies within the interval.
To calculate the confidence interval, we take the area under the curve. Then, starting at the maximum point, which is the score, we move outward until we get an area that is 90% of the full area under the curve. The interval is always centered on the peak.
To convert the low and high points of the confidence interval from a Theta scale to a Scale Score scale, you use the same slope and intercept as used before.
We will illustrate this with the results of the first test. Recall that it has a score of 0.4. The confidence interval is from -1.08 to 1.48. The Scale Score is 1540 with a confidence interval from 1392 to 1688.
The difference between the top or bottom of the interval and the score is the standard error. In this case, the standard error of the Theta core is 1.48 and the standard error of the scale score is 148. Notice that scale score standard error is Theta standard error times the slope from the conversion function; 100 in this case.

The second test result has a Theta Score of -0.6 and a confidence interval from -2.87 to 1.67 (Standard Error ±2.27). The Scale Score is 1440 with a confidence interval from 1213 to 1667 (Standard Error ±227).

The second student answered harder questions correctly while missing easier questions. Intuitively this should lead to less confidence in the resulting score and that is confirmed by the broader confidence interval (larger standard error).
Disadvantages and Advantages to IRT Test Scoring
IRT Test Scoring is complicated to perform, to explain, and to understand. The math requires numerical methods that are impractical without computers.
Perhaps the biggest weakness is that this form of scoring works best when questions span a broad range of skill levels. That makes it less suitable for mastery assessment which benefits more from a threshold test.
For achievement testing, there are important advantages. Multiple tests can be calibrated to the same scale, supporting the measurement of growth year over year. Calibration of assessment items ensures that scores of different student cohorts are comparable even as the test itself is updated with new questions. And the scoring system is compatible with computer adaptive testing.
Wrapup
Next time you encounter a standardized test score you'll have a better idea of how it was calculated. And, hopefully that will give you a better understanding of how to interpret the score and what to do with it.
There are many types of assessment and corresponding ways to score them. Overall, it's important ensure that the form of testing and scoring is well-suited to the way the results will be interpreted and applied.
References
- "Ability Estimation with Item Response Theory", Nathan A. Thompson, Ph.D, 2009.
- "Smarter Balanced Scoring Specification", Prepared by the American Institutes for Research, 2014.
No comments:
Post a Comment